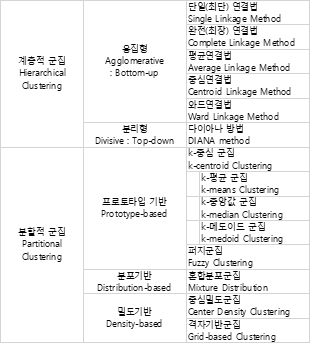
1. 군집분석

	차이
요인분석	유사한 변수를 함께 묶어주는 것
판별분석	사전에 집단이 나누어져 있는 자료를 통해, 새로운 데이터를 기존의 집단에 할당
군집분석	군집의 개수/구조에 대한 가정 없이 데이터들 사이의 거리를 기준으로 군집화 유도

2. 거리

3. 계층적 군집분석

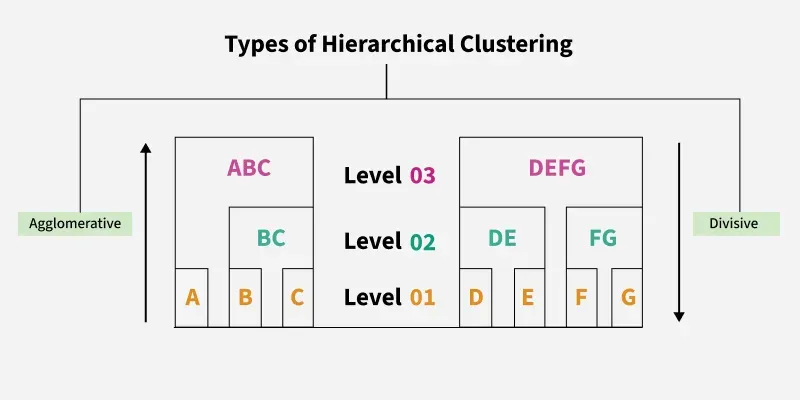
$n$ 개의 군집으로 시작해 점차 군집의 개수를 줄여 나간다.

Agglomerative (합병형), bottom-up
divisive (분리형), top-down

	설명
최단연결법 (Single Linkage)	$n * n$ 거리행렬에서 거리가 가장 가까운 데이터로 군집 최단거리 (min) 을 거리로 계산해 거리행렬 수정 진행 수정된 거리행렬에서, 거리가 가까운 데이터/군집을 새로운 군집으로 형성
최장연결법 (Complete)	최장거리 (max)
평균연결법 (Average)	평균 (mean)
와드연결법 (Ward)	군집 내 편차들의 제곱합을 고려. 군집 간 정보의 손실을 최소화하기 위해 군집화를 진행
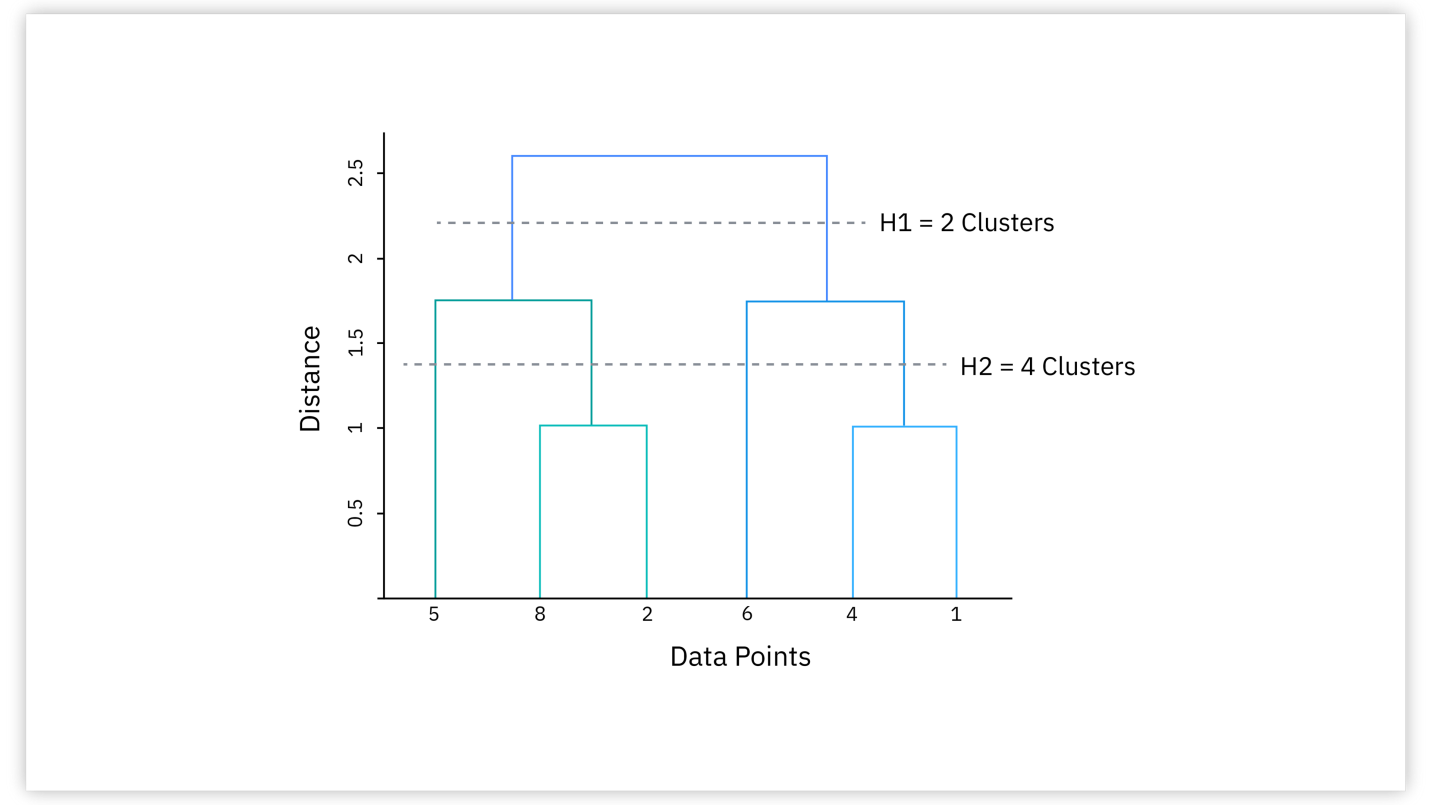
군집화	거리행렬을 통해 가장 가까운 거리의 객체들간의 관계를 규명하고 덴드로그램을 그린다. 덴드로그램을 보고 군집의 개수를 변화해가면서 적절한 군집수를 선정한다. 군집수는 분석 목적에 따라 선정할 수 있으나, 5개 이상의 군집은 잘 활용하지 않는다.

4. 비계층적 군집분석

$n$ 개의 개체를 $k$ 개의 군집으로 나눌 수 있는 모든 가능한 방법을 점검해 최적화된 군집 형성.

KMC

5. 혼합분포군집

Mixture Distribution Clustering

model-based (모형 기반) 군집 방법 데이터가 특정 모집단 모형 $X$ 으로부터 나왔다는 가정 하에서, 모수와 함께 가중치를 자료로부터 표현하는 방법을 사용한다.

모형 $X$ 는 $k$ 개의 모수적 모형의 가중합으로 표현
- 흔히 정규분포 / 다변량 정규분포를 가정 $k$ 개의 각 모형은 군집을 의미하며, 각 데이터는 추정된 $k$ 개의 모형 중 어느 모형으로부터 나왔을 확률이 높은지에 따라 군지의 분류가 이루어진다. 흔히 혼합모형에서의 모수와 가중치의 추정 (최대가능도추정) 에서는 EM 알고리즘이 사용된다.


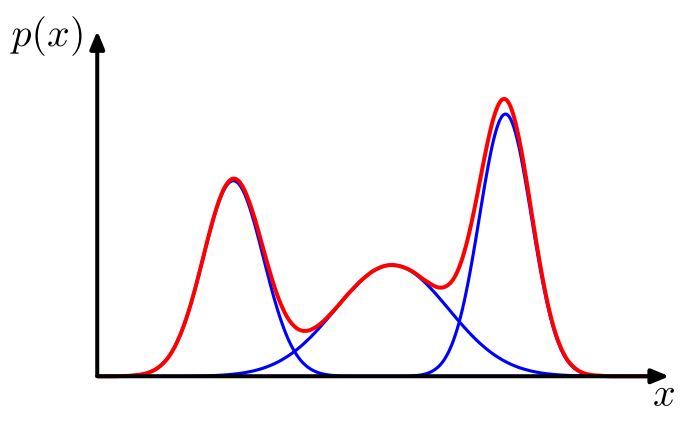	다봉형이므로 단일 분포로는 설명할 수 없으며, 대략 3개 정도의 정규분포로 설명 가능 반드시 정규분포로 제한할 필요는 없다.
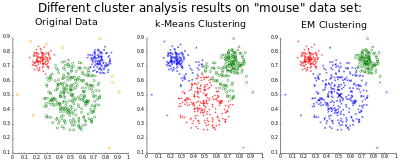	여러개의 이변량 정규분포 결합을 통해 설명 가능. 반드시 정규분포로 제한할 필요는 없다.

EM 알고리즘

6. SOM

8. Resampling

재표본추출

가지고 있는 데이터에서 표본을 수많이 재추출하고, 재추출된 표본에 모형을 적합하게 함으로써 생성된 분류기의 성능 측정에 대한 통계적 신뢰도를 높이는 방식

a. k-fold Cross Validation

데이터를 k개의 집단으로 나눈 뒤
- k-1 개의 집단으로 분류기 학습
- 나머지 1개의 집단으로 분류기 성능 테스트
위 작업을 k 회 반복한다.
k 번의 테스트를 통해 얻은 MSE 값의 평균을, 해당 모델의 MSE 값으로 활용한다.

b. bootstrap

c. holdout

9. 군집화 기법 종류

밀도기반 군집분석

어느 점을 기준으로, 주어진 반경 냉 최소 개수만큼의 데이터들을 가질 수 있도록 하는 것으로, 특정 밀도함수 혹은 밀도에 의해 군집을 형성해나가는 기법

DBSCAN
- 밀도 한계점에 따라 군집을 형성해나가는 대표적인 밀도기반 군집화 기법
- 군집화와 동시에 noise 를 표시하는 것으로, 데이터를 보다 정확하게 이해 가능
OPTICS
- 군집화 구조 식별을 위해, 부가적 순서를 생성하는 밀도기반 기법
DENCLUE
- 밀도 분포함수에 기반한 군집화방법

격자기반 군집분석

데이터가 존재하는 공간을 격자구조로 이루어진 유한개의 셀들로 양자화한 뒤, 데이터 포인트 대신 셀을 이용해 군집화 과정을 수행하는 기법. 빠른 처리시간을 가지며, 데이터 내 객체 수에 독립적이고 양자화된 공간의 각 차원에서 셀의 수에만 의존한다

STING 격자 셀에 저장되어 있는 통계정보를 탐색하는 격자기반 기법
WaveCluster Wavelet 변환 기법을 사용하여 객체들을 군집화하는 격자기반 기법
CLIQUE 고차원 데이터 공간의 군집화를 위한, 격자 및 밀도기반 기법

10. 군집분석의 타당성 지표

a. 실루엣 (Silhouette)

s (i) = \frac{b ( i ) - a ( i )}{max { a ( i ) , b ( i )}}

$a (i)$ : $i$ 번째 개체와 같은 군집에 속한 요소들 간, 거리들의 평균
$b (i)$ : $i$ 번째 개체와 다른 군집에 속한 요소들 간, 거리들의 평균을, 군집마다 구했을 경우의 최솟값

군집 내의 응집도 / 군집 간 분리도를 이용한 지표

군집 내 요소간의 거리가 짧고, 다른 군집 간 거리가 멀수록 값이 커진다
완벽한 군집화가 이루어졌을 경우 1, 군집화가 전혀 이루어지지 않았을 경우 -1

b. Dunn Index

Dunn Index = \frac{min ( inter-cluster distances )}{max ( intra-cluster distances )}

Dunn Index 는 클수록 군집이 잘 형성되었다.

Quartz 4

Explorer

045. 군집분석