의사결정나무

분류함수를 의사결정 규칙으로 이루어진 나무 모양으로 그린다. 의사결정 문제의 시각화. 계산결과가 의사결정나무에 바로 나오므로 해석이 간편. 의사결정나무는 주어진 입력값에 대하여 출력값을 예측하는 모형

• 분류나무 모형
• 회귀나무 모형

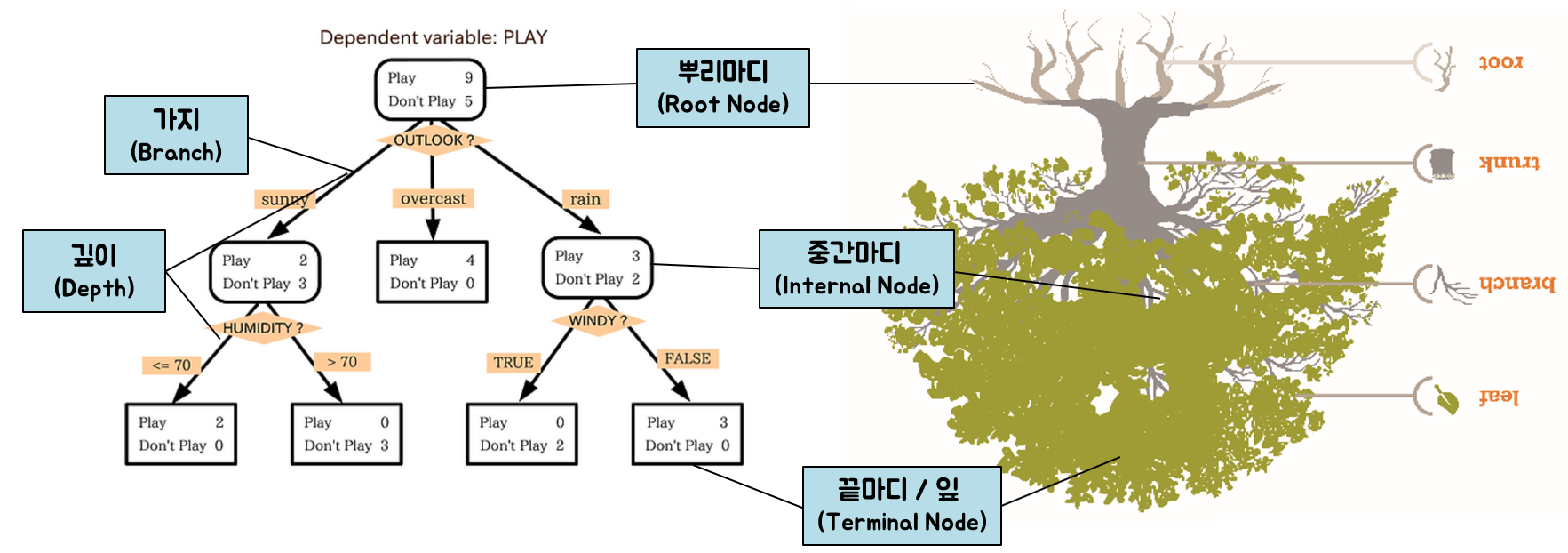
• 구성요소
  • 뿌리마디
  • 자식마디
  • 부모마디
  • 끝마디
  • 중간마디
  • 가지 (Branch)
  • 깊이 (Depth)

중시/치중하는 성질	상황
예측력	기대집단의 사람들 중 가장 많은 반응을 보일 고객의 유치방안을 예측	고객유치
해석력	심사 결과 부적격 판정이 나온 경우, 고객에게 부적격 이유를 설명	신용평가

• 활용
  • 세분화
    • 데이터를 그룹으로 분할해 그룹별 특성 발견
  • 분류
    • 관측개체의 목표변수 범주를 몇개의 등급으로 분할
  • 예측
    • 규칙을 찾아내기
  • 차원축소 / 변수선택
  • 교호작용효과 (Interaction Effect) 파악
    • 범주의 병합 목적
    • 연속형 변수의 이산화 목적

장점	단점
결과 설명 용이	새로운 자료에 대한 overfitting 위험성
모형제작이 계산적으로 복잡하지 않음	분류 경계선 부근의 자료값에 대해 오차 큼
대용량 데이터에서도 빠름	설명변수 간의 중요도 판단 어려움
비정상 noise 데이터에서도 민감함 없이 분류 가능
상관성이 높은 다른 불필요 변수가 있어도, 크게 영향받지 않음
설명 / 목표변수에 수치형 / categorical 모두 사용 가능
모형 분류 정확도 높음

• 분석과정
  • 성장 - 가지치기 - 타당성 평가 - 해석/예측

나무의 성장

훈련자료는 $(x_i,y_i),i=1,\dots ,n$. 이때 $x_i=(x_{i1},\dots ,x_{ip})$.

나무모형의 성장과정은, $x$ 들로 이루어진 입력공간을 재귀적으로 분할하는 과정.

$$R_1(j,A)=x_i\in A,R_2(j,A^c)=x_i\in A^c$$

1) 분리규칙 (Spliting Rule)

최적 분할의 결정은 불순도 감소량을 가장 크게 하는 분할이다. 각 단계에서 최적 분리기준에 의한 분할을 찾은 다음, 각 분할에 대해서도 동일한 과정을 반복한다.

$$\Delta i(t)=i(t)-p_L\ast i(t_L)-p_R\ast i(t_R),i(t)=\sum _{i\in t}(y_i-\overline{y_t})$$

분리변수 (Split Variable) 가	가능한 분리규칙 case
연속형인 경우	$A=x_j\le s$
범주형 $\{1,2,3,4\}$ 인 경우	$A=1,2,4$ 와 $A=3$

2) 분리기준 (Splitting Criterion)

• 이산형 목표변수

기준값	분리기준
chi2 통계량 p값	p값이 가장 작은 예측변수와, 그때의 최적분리에 의해 자식마디 형성
지니지수	지니지수를 감소시키는 예측변수와, 그때의 최적분리에 의해 자식마디 형성
엔트로피지수	엔트로피지수가 가장 작은 예측변수와, 그때의 최적분리에 의해 자식마디 형성

• 연속형 목표변수

기준값	분리기준
ANOVA 에서 F 통계량	p값이 가장 작은 예측변수와, 그때의 최적분리에 의해 자식마디 형성
분산의 감소량	분산의 감소량을 최대화하는 기준의, 그때의 최적분리에 의해 자식마디 형성

정지규칙 (Stopping Rule)

더이상 분리가 일어나지 않고, 현재의 마디가 끝마디가 되도록 하는 규칙.

• 정지기준 (Stopping Criterion): 의사결정나무의 깊이 (Depth) 를 지정, 끝마디의 레코드 수의 최소개수를 지정한다.

나무의 가지치기 (Pruning)

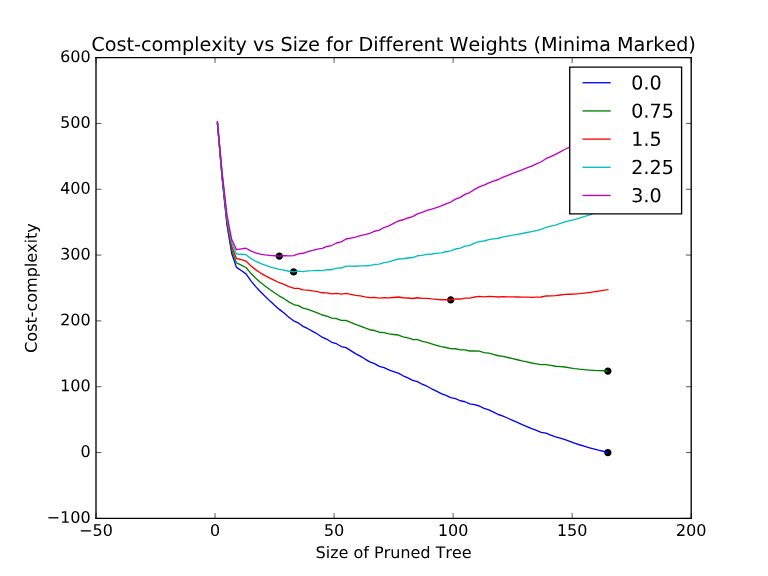
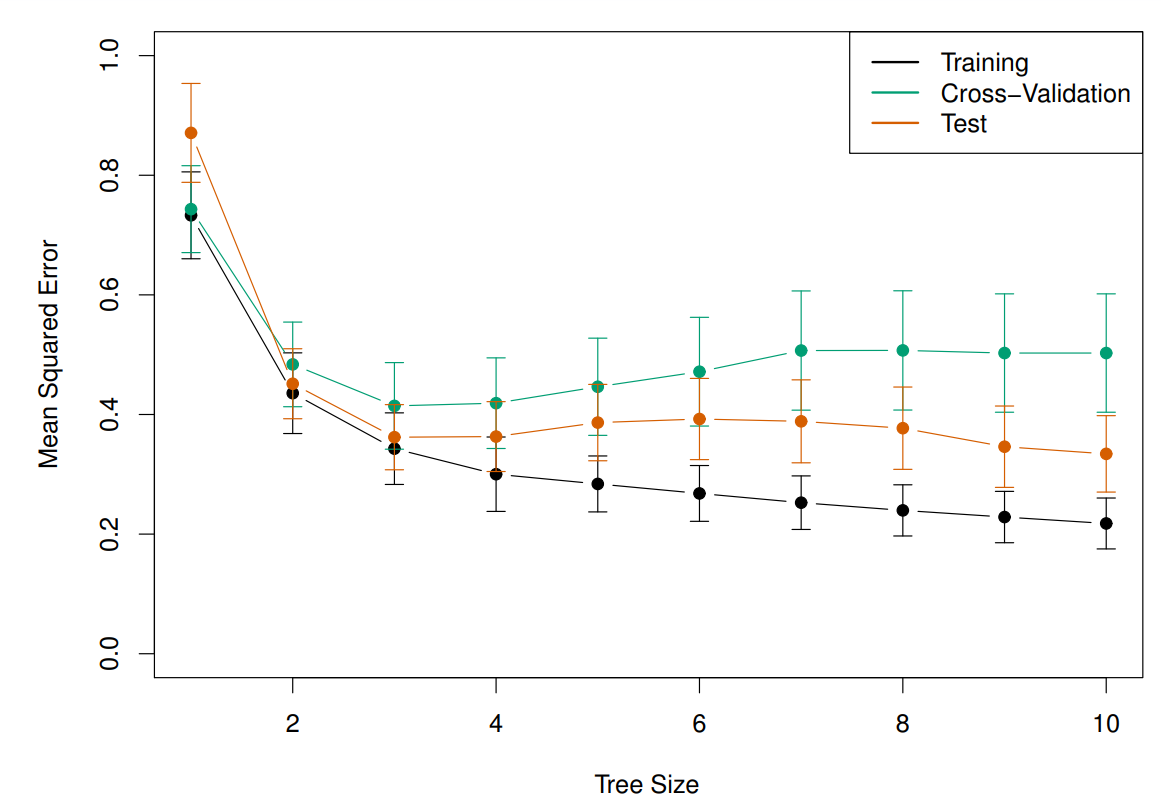
• 나무모형의 크기 $\propto$ 모형의 복잡도:
  • 최적의 나무 크기는 자료로부터 추정하게 된다.
  • 너무 크다 - overfit
  • 너무 작다 - underfit

• 일반적으로 사용하는 방법은,
  • 마디에 속하는 자료가 일정 수 이하 (ex. 5) 일 때
    • 분할을 정지하고
    • 비용-복잡도 가지치기 (Cost-Complexity Pruning) 을 이용하여 성장시킨 나무를 가지치기하게 된다.

---

불순도의 여러가지 측도

• 목표변수가 categorical 일 때 기준

chi2 통계량	${\chi }^2={\sum }_{i=1}^k\frac{(O_i-B_i{)}^2}{B_i}$ $k$ 는 범주의 수, $O_i$ 는 실제도수, $B_i$ 는 기대도수, $B_i=$ (열의 합계 * 합의 합계) / 전체합계
지니지수	$Gini(T)=1-{\sum }_{l=1}^k{p}_l^2$	노드의 불순도를 나타내는 값. 값이 클수록 이질적 (diversity) 순수도 (purity) 가 낮다고 볼 수 있다
엔트로피지수	$Entropy(T)={\sum }_{l=1}^k{p}_l\ast lo{g}_2(p_l)$	열역학의 개념. 무질서한 정도에 대한 측도. 값이 클수록 순수도 (purity) 가 낮다고 볼 수 있다.

의사결정나무 알고리즘

			불순도의 측도
CART	위에서 설명된 방식을 그대로 답습. 가장 메이저하다.	개별 입력변수만이 아니라, 입력변수의 선형결합 중에서 최적의 분리를 찾을 수 있음	출력(목적) 변수가 categorical 이면 지니지수 출력(목적) 변수가 연속형 이면 이진분리 (Binary Split)
C4.5 C5.0		CART 와는 다르게 각 마디에서 다지분리 (Multiple Split) 가 가능하다. categorical 입력변수에 대해서는 범주의 수만큼 분리가 일어난다	엔트로피지수
CHAID		가지치기를 진행하지 않는다. 적당한 크기에서 나무모형의 성장을 중지한다.	출력(목적) 변수가 categorical 이면 chi2 통계량 출력(목적) 변수가 연속형 이면 F 통계량