Hypothesis Test
| 통계적 가설 | Statistical Hypothesis | 관심있는 population의 성질에 대한 단정이나 추측 등의 표현 (statement) 이러한 가설은 흔히 모집단의 성질을 나타내는 rv의 분포에 대한 표현으로 나타난다. | | 단순가설 | Simple Hypothesis | 어떤 가설이 확률분포 (pd) 를 완전히 결정한다 | | 복합가설 | Composite Hypothesis | 그렇지 않다 |
다양한 검정법에서 우선순위를 정하는 것은 옳은 결론을 내리는 빈도가 높은, 즉 잘못된 결정을 내릴 확률이 낮은 검정법이 좋은 검정법이라는 것.
검정통계량(Test Statistics): 주어진 rs에 근거하여 통계적 가설에 대한 증거를 살펴볼 때 사용되는 통계량
기각영역(Rejection Region, Critical Region): 를 기각하게 되는 검정통계량의 값을 가지는 sample space의 부분집합 (event)
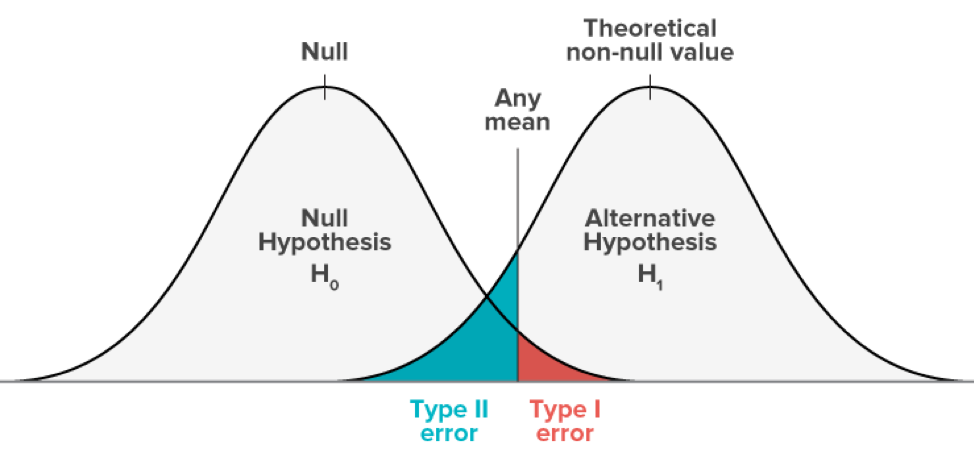
| True | False | |
|---|---|---|
| reject | Type 2 Error () 유죄인데 석방 | |
| accept | Type 1 Error ()무죄인데 사형 |
제1종 오류를 범활 확률 는 유의확률(Significance Level) 라고 따로 칭함. 은 기존으로부터의 변화이므로 채택에 있어 훨씬 엄격해야 함. 따라서 가 보다 훨씬 더 중시됨.
let Rejection Region . then
This can also be written as Loss Function.
Power Fucntion
여기서, 에 대한 기각영역이 인 test의 검정력함수 (power function)은 이하와 같다. 즉, 이는 를 기각하는 확률로 정의된다.
이는 패러미터 의 참값이 무엇이냐에 따라 다른 값을 가지므로 의 함수이다.
주어진 에서의 power function의 값 은 이 에서의 검정력 (power).
power는 를 기각할 확률.
- if , power는 작을수록 좋다.
- , 이 경우 power .
- if , power는 클수록 좋다.
- , and 이 simple hypothesis, 이 경우 power .
이와 같이 power function은, 마치 MSE가 점추정의 기준이 되었던 것처럼, (유의수준)이 고정되었을 때 test 방법의 성능을 결정하는 기준이 된다.
Significance Probability (p-value)
앞에서 언급했던 것과 같이, 좋은 검정법을 찾기 위해 sample space를 와 채택영역 로 나누고 와 를 계산하여 오류의 확률을 작게 만드는 검정법을 고르게 된다. 사용할 검정법을 결정하고 나면, 자료에서 관측된 값이 에 속할 경우 를 기각하고, 이외에는 를 기각하지 않는다고 결론을 내리게 된다. 그런데 관찰된 test stat의 값이 에 속한다 하더라도 값의 크기 등에 따라 통계적 유의성에 대한 의미가 다를 수 있다. 따라서 기각할 것인지, 하지 않을 것인지 이분법적인 결론만을 제시하기보다, 관측한 자료가 에 대하여 어느 정도의 반증이 되는지를 수치적으로 나타낼 수 있는 (유의확률)을 이용하여 test의 결론에 이르는 경우가 많이 있다.
p값 (p-value), 즉 관측된 유의수준 (observed significance level), 혹은 유의확률 (Significance Probability), 는 가 참이라는 가정 하에, 우리가 관측한 값과 같거나 더 극단적인 값을 얻을 확률 (ex. ) 로 정의된다. 여기서 더 극단적이라는 것은, 관측한 값보다 에 더 가까운 것을 의미한다. 만약 어떤 관측값에 대하여 p값을 계산하였더니 아주 작은 값이 나왔다면, 우리가 관측한 값 자체가 이미 매우 극단적이라서 이보다 더 강한 에 대한 증거를 관측할 확률이 작다는 것이다. 즉, 관측값이 하에서 나오기 어려운 값이라는 뜻이므로 를 기각할 근거가 된다고 할 수 있다. 만약 어떤 관측값에 대하여 p값을 계산하였더니 작지 않은 값이 나왔다면, 우리가 관측한 값이 하에서 흔히 나올 수 있는 값이라는 것이고, 즉 를 기각할 근거가 되지 않는다고 할 수 있다.
p값이 를 기각할만큼 작은지를 결정하는 것은 보통 결과를 해석하는 사람에게 달려있다. 그러나 가설검정을 할 때는 흔히 적당한 유의수준 의 값을 생각하고 있기 마련이므로, p값이 보다 작으면 관측된 자료가 대립 가설에 대한 충분한 증거가 된다고 판단하여 를 기각하게 된다. 정리하자면, p값은 하에서 test stat의 관찰값 (test stats) 이 를 기각하는 방향으로 나타나는 확률을 의미한다. 주어진 유의수준 보다 p값이 작으면 를 기각하며, 그렇지 않은 경우에는 를 받아들이게 된다.
Optimal Testing Method
항상 옳은 결과를 가져다주는 검정법을 사용할 수 있다면 가장 좋겠지만, 샘플에서 주어지는 정보만을 가지고 모집단의 특성에 대한 결론을 내려야 하는 상황에서 언제나 옳은 결과를 가져다주는 test 방법을 찾을 수는 없다. 그렇기에 이 장의 목표는 옳은 결과를 가져다주는 빈도가 높은 test 방법을 찾는 것이 된다. 잘못된 결론을 내릴 확률은 두 가지 오류로 표현되므로, 제 1종 오류와 제 2종 오류의 발생확률을 낮게 하는 test 방법을 찾아야 한다. 불행히도, 샘플의 크게가 정해져 있는 경우 둘 다를 최소로 하는 test 방법을 찾는 거은 불가능하다. 예를 들면, 를 최소로 하는 가장 간단한 방법은 언제나 를 채택하는 것이지만 (), 이는 에서의 power를 0으로 최소화시키고, 즉, 를 극대화시킨다.
let .

이때. 에서의 power는 유의수준 와 같고, 일 경우에는 . 이인즉
따라서 와 의 경계점에서 이 된다. 즉, 샘플의 크기가 일정할 때 를 줄이고자 하면 경계점에서 의 값이 커지며, 이 역 또한 성립한다. 이를 power로 표현하면, 하에서 power는 큰 것이 바람직하나 power 를 늘이고자 하면 의 값이 같이 커지게 되므로 제1종 오류의 확률 ()의 확률을 최소화하면서 power를 최대화하는 일은 sample의 크기가 정해져 있는 경우 불가능하다.
만약 sample의 크기를 늘인다면, 의 값을 고정시킨 상태에서 주어진 하에서의 값에서의 power를 크게 할 수 있다.
이 절에서는 power function 을 기준으로 하는 Optimal Testing Method (최량검정법)에 대해 살펴볼 것이다. 우선, 와 이 모두 simple인 경우를 생각해보자. 위에서 이야기하였듯 를 최소화하면서 하에서의 power를 최대화하는 것은 불가능하므로, 이에 대한 합리적 대안으로 (제1종 오류를 범할 확률)을 주어진 작은 값으로 제한한 상태에서, power를 최대화하는 의미에서의 OTM을 다음과 같이 정의한다.
에 대한 rejection region 가 다음 조건을 만족할 때 이를 유의수준 에서의 MPT의 RR, 또는 MPRR이라고 한다.
가 에 해당하는 power function이라 하면,
- ,
- .